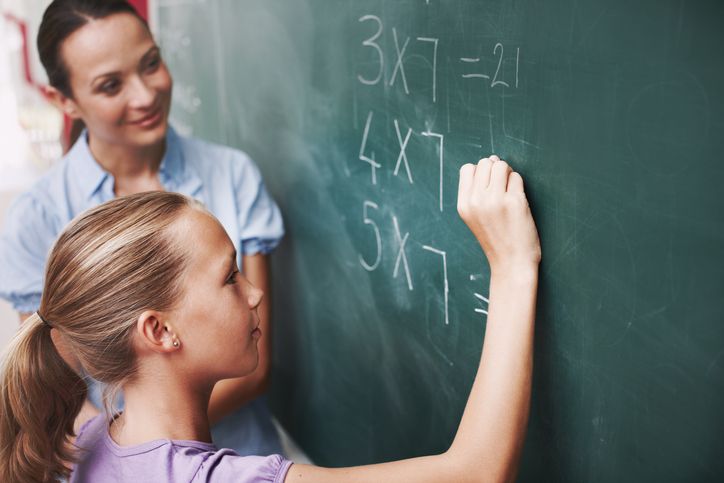What does ‘fluency’ mean to you? We asked teachers for their definition.
Long read
Until we all agree on what we are trying to achieve with procedural fluency, how can we hope to achieve it?
In a thought-provoking conversation last year, Dr. Nicki Newton made a statement that lingered, “Speed has hijacked the fluency conversation.” It’s a phrase that’s stuck with me, highlighting the complexities of what we understand as “fluency” in mathematics.
Delving deeper
So I decided to delve deeper, running a poll across social media platforms to gauge teachers’ perceptions of fluency. With a thousand educators participating, the results offered a panoramic view of diverse perspectives.
As a mathematics/stats major, I’m the first to poke holes in the methodology of the poll. But the purpose wasn’t to perform an in-depth statistical analysis, but rather, just to get a birds eye view on what different perspectives were out there. Firstly, thank you to those who participated. You can see the results below. Keep in mind, the example case was multiplication facts (times tables).
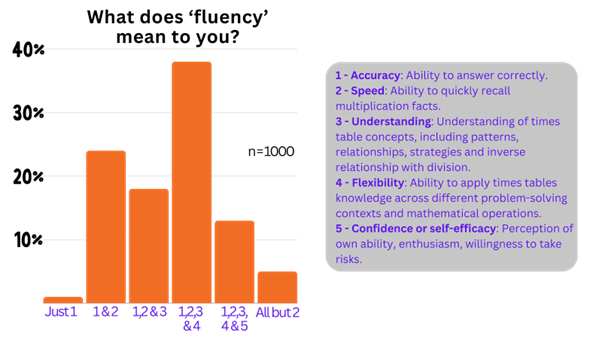
Without giving too much attention to this, it highlights that, as an educational community, we don’t have a common understanding of what the term ‘fluency’ means.
Let’s just clarify that we’re talking about ‘procedural fluency’. We’ll keep using the multiplication facts example case for consistency.
Exploring the data (and the passionate comments!), we can see a continuum appearing. On one end we have those who believe it’s all about speed (quick recall). On the other are those who believe conceptual understanding is all that matters.
So what is procedural fluency then? Speed or conceptual understanding? Or somewhere in between? And is the order in how we get to procedural fluency important?
These are the questions we’ll attempt to answer in this piece.
In order to do so, we need to, first, hold a common definition of what procedural fluency actually is.
So what exactly is Procedural Fluency?
Up front, let’s establish some common ground. I think we can all agree that to obtain procedural fluency, we need our students to be efficient at answering multiplicative facts. That is, we need students to be able to use multiplication facts in a reasonable amount of time so that it doesn’t impede them in solving problems.
I would really recommend reading work of leading ‘fluency’ researchers and practitioners, Jennifer Bay-Williams & John San Giovanni. John helped me to distil their overall message down to this:
Procedural fluency in mathematics is flexibility, efficiency, and accuracy while incorporating reasonableness. Fluency is grounded in conceptual understanding. It involves students’ ability to choose appropriate strategies, apply them efficiently, and understand the underlying concepts behind mathematical operations.
They advocate for a balanced approach to fluency construction focusing on conceptual understanding of operations, number concepts, and computational strategies so that students both understand strategies and can decide when they’re useful.
Please, dig into their research. It is thorough, insightful and practical.
I find this to be the most comprehensive and accurate definition of the procedural fluency our students need. As someone who spends my time researching mathematics education with a particular emphasis on reducing the impacts of mathematics anxiety, I’d like to draw out some implications for us as educators whilst, at the same time, providing supporting arguments for this definition.
Students don’t build procedural fluency on conceptual understanding alone.
We need our students to be efficient at answering multiplicative facts. Without a certain level of efficiency, students will struggle and stall when needing this fact fluency as part of a larger problem.
There is a recent phenomenon where many well-intentioned teachers have placed too much emphasis on conceptual understanding alone.
I spoke with Kim Swaney Montague from Math is Figure-out-able and she explained that the push for conceptual understanding was so strong, that the need to build procedural fluency became less explicit and even forgotten.
Kim elaborated, “Teachers heard “don’t do speed work” and just stopped everything, thinking kids will get there on their own. It doesn’t happen.”
We must be deliberate at building this procedural fluency. But what does that look like if conceptual understanding of concepts is alone, not enough.
Implication 1: Focusing on conceptual understanding alone will not lead to procedural fluency
There is a recent phenomenon where many well-intentioned teachers have placed all emphasis on conceptual understanding alone. I spoke with Kim Swaney Montague from Math is Figure-out-able who explained that the push for conceptual understanding was so strong that the need to build procedural fluency became less explicit and even forgotten.
Kim elaborated, “Teachers heard “don’t do speed work” and just stopped everything, thinking kids will get there on their own. It doesn’t happen.”
Now don’t get me wrong, I am a huge advocate for conceptual understanding. As we saw earlier, procedural fluency must be grounded in this conceptual understanding and it’s a fantastic place to start. But alone, it doesn’t foster efficiency or automaticity. We must be deliberate at building this automatic aspect of procedural fluency.
For example, a student may conceptually understand that 6 x 8 = 48. They can draw an array, can skip count their way there with no problems. However, it takes significant cognitive load and time to arrive there. If this multiplication fact was a small part of a much larger question, this can cause cognitive overload and induce anxiety itself.
Procedural fluency plays a crucial role in mitigating this cognitive overload by reducing the cognitive burden associated with basic mathematical operations. Cognitive load theory, suggests that learners have a limited working memory capacity for processing new information.
When learners are required to simultaneously manage complex procedures or algorithms without automaticity, it can overwhelm their working memory, leading to cognitive overload.
Procedural fluency means students can perform basic operations, or in this case, multiplication facts, without conscious effort. When students have achieved procedural fluency, these basic operations become automatic, requiring minimal cognitive resources to perform.
As a result, students can allocate more cognitive capacity to higher-order thinking tasks, such as problem-solving, reasoning, and making connections between mathematical concepts.
By reducing the cognitive load associated with routine mathematical operations, procedural fluency allows students to focus their attention on understanding mathematical concepts deeply and applying them in various contexts.
This not only enhances learning efficiency but also fosters conceptual understanding and long-term retention of mathematical knowledge. Thus, procedural fluency serves as a scaffold for cognitive development in mathematics, enabling students to tackle more complex problems with confidence and fluency.
Implication 2: Focusing on speed (quick recall) and accuracy only will not lead to procedural fluency
Firstly, I would again like to reiterate, we all want our students to become efficient and ‘automatic’ (with their multiplication facts for example.) But we must consider how we get there. In the words of former NCTM president, Linda M. Gojak, “Fluency entails so much more than being fast and accurate!”
The current NCTM position statement explains that, “Conceptual foundations lead to opportunities to develop reasoning strategies, which in turn deepens conceptual understanding.” Whereas memorization alone does not facilitate understanding at all, even if there is quick recall.
It is worth exploring the work of Katherine Cartwright in this regard. In her 2018 paper she expresses the notion that you can possess conceptual understanding without speed but not the other way around. As students become more procedurally fluent (in its above definition) they will also increase automaticity/speed, but not the other way around.
Focusing on speed/quick recall alone or even first in the journey can lead to dire consequences for students.
Lynn McClure references the misunderstanding of current US curriculum aims that state, students will “become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately.”
She then goes on to say that The problem is that many schools are interpreting this as practice, practice, practice of rote learned memorization. This leads to a pretty rigid and boring mathematical diet and is not what is intended in the aims.
If we equate only speed with fluency, there is a real temptation for the endless pursuit of quick recall. I’ve seen classes, more than I can count, obsessed with speed. It’s literally drill and kill. And whilst well-meaning, the impacts can be disastrous, and in fact, far worse than lessons just being rigid and boring!
Let me briefly outline 3 ways we now know this can harm students.
Firstly, it contributes to unhelpful attitudes towards mathematics. Mathematics is about far more than just being fast and it’s not just about getting the right answer. Real world mathematics is often a place where problems need to be solved with creativity and perseverance, often taking a long time.
In fact, historically, many of the theorems we teach in a lesson took decades to derive. Mathematics also ought to be a place where students can feel safe to take risks and learn from their mistakes. Learning from mistakes and error-analysis is one of the best ways to build understanding.
Sadly, many students and even adults can track their anxiety or hatred of maths back to times tables competitions, timed tests, or public charts that for those not at the top, only induce shame.
Secondly, as Jennifer Bay-Williams helpfully explains in this insightful chat on the ‘Make Math Moments’ podcast, memorizing facts without understanding is stress inducing. She likens it to that all-too-familiar experience of forgetting phone numbers when under pressure.
When we pair this with the main other stress inducer, time pressure, then it’s no wonder why the experience can be so detrimental. When speaking with Pam Harris from Math is Figure-out-able, she summarised the research in the space by saying, “when students are feeling shame, the thinking part of their brain shuts off.
They can’t retrieve from rote memory, they can’t think clearly. That fight or flight has kicked in.” And we know from neuroscience that this is, in fact, the amygdala kicking in, shutting off the thinking parts of our brain (pre-frontal cortex) as if we were actually in physical danger.
Thirdly, only rote learning facts means that the use of that fact is completely limited in its application. Kilpatrick et al (2001) takes the stance that separating procedures (skills) from understanding can have dire results, “students who learn procedures without understanding can typically do no more than apply the learned procedures, whereas students who learn with understanding can modify or adapt procedures to make them easier to use”.
On the contrary , “When students use a procedure they do not understand, they are more likely to make errors and fail to notice when the answer does not make sense” to reference the NCTM once more.
Let me attempt to explain with an example.
6 x 8 = 48
This basic fact, if learned only by rote, allows me to regurgitate it only when it looks exactly like that. I’ve seen many students who can answer this question within a second but from here they can’t tell me 8 x 6. They can’t tell me the factors of 48.
They can’t answer 48 divided by 8. If, under stress, they accidentally answer 38, they cannot notice that something is wrong. They can recall this fact in lightning speed, but have not procedural fluency.
Procedural fluency would mean understanding the relationships and connections and that’s what leads to flexibility.
A student who has procedural fluency knows that 8 x 6 is the same as 6 x 8. They infer that 6 and 8 are factors of 48… and therefore so are 2,3, and 4. They can surmise that 48 ÷ 8 is 6. They understand that a rectangular array could represent 48 with side lengths 6 and 8 and explore other combinations.
They use 6 x 8 to quickly get to 7 x 8 by adding another 8. They deduce that 3 x 16 would achieve the same result. If they did write 38 accidentally, they would immediately see that 6 x 8 must be greater than 5 x 8 which is 40 and therefore, adjust their thinking. This is the type of fluency that helps students to build a strong foundation where they can use 6 x 8 as part of their strategy for more intricate problems later.
Procedural fluency with conceptual understanding also means that retention is increased as this fact becomes part of their ever increasing web of understanding. It’s all connected.
I love what Field’s medal winner, William Thurston, said about this:
“Mathematics is amazingly compressible: you may struggle a long time, step by step, to work through some process or idea from several approaches. But once you really understand it and have the mental perspective to see it as a whole, there is often a tremendous mental compression.
You can file it away, recall it quickly and completely when you need it, and use it as just one step in some other mental process. The insight that goes with this compression is one of the real joys of mathematics.” Really understanding multiplication facts in this sense, means one needs to possess procedural fluency. This requires practice in different contexts to gain the flexibility.
It also means interleaving the practice in order to increase retention.
Maths is a cumulative subject where often concepts build upon the previous concepts. Genuine procedural fluency acts as the foundation upon which higher-level maths skills are constructed. Imagine a student trying to solve a complex equation or tackle a multi-step problem.
If they’re not flexible with basic arithmetic operations, it can derail their entire process. Building fluency leads to a student being efficient, allowing students to focus on the higher-order thinking required to solve complicated mathematical problems.
Again, I defer to Thurston’s wisdom:
“One feature of mathematics which requires special care in education is its ‘height,’ that is, the extent to which concepts build on previous concepts. Reasoning in mathematics can be very clear and certain, and, once a principle is established, it can be relied on.”
“The structure is not like a tree, but more like a scaffolding, with many interconnected supports. Once the scaffolding is solidly in place, it is not hard to build it higher, but it is impossible to build a layer before previous layers are in place.”
So how can we build this true procedural fluency?
Rather than trying to answer this here and barely scratching the surface, I’ll give a few thoughts and then point you in the direction of where you can learn more.
Firstly, advice from Jennifer Bay-Williams. Build automaticity through strategy. Put students in decision making positions where they need to choose the most efficient strategies. In the ‘Make Math Moments’ podcast, Kyle speaks about practising through reasoning and strategy and advocates for building automaticity this way rather than starting with speed. Jennifer expands by saying the benefits are also that students build number sense and confidence along the way.
Secondly, help students to make connections to what they already know; that scaffolding to which Thurston alluded to. Some fantastic ways I see this happening are ‘thin slicing’ which is popular among teachers familiar with the ‘Building Thinking Classrooms’ research.
Pam Harris does something similar called Problem Strings and they are a fantastic way of facilitating a rich learning experience connecting what students already know to the new content they’re learning. They’re like “high dosage patterning” for students.
Peter Sullivan states that procedural fluency, “can be developed in two ways: by short everyday practice of mental processes; and by practice, reinforcement and prompting transfer of learnt skills.” He goes on to contrast, what he calls, mechanical with automatic skills practice.
With mechanical practice, students have limited capacity to adapt the learnt skill to other situations. With automatic practice, built on understanding, students can be procedurally fluent while at the same time having conceptual understanding. Mike Askew gives some helpful advice in that this practice “is best done little and often rather than in less frequent, longer blocks of time.”
Thirdly, cultivate a safe risk-taking environment in your classrooms. Do this by celebrating the learning and not the performance; value thinking, effort, progress and creativity. Avoid shame and fear inducing activities like rote memorization, timed tests, public score charts and making mathematics a subject where only getting the right answer is valued. By creating a safe space for taking risks, you empower your students to embrace challenges and grow without fear of judgment or failure.
But what if a student still doesn’t have quick recall by the time they ‘should’?
I completely resonate with this concern. I’ve had students who get completely derailed when solving algebraic equations because they aren’t efficient in the multiplication facts part of the question.
I’ll say just a couple of things and I hope some discussion might arise as to how we can do this well.
Firstly, I’m always conscious of getting caught up with the ‘where a student should be at’. Students learn at different paces. And this completely depends on your curriculum as well. For example, in some countries (like Singapore), students are solving algebraic equations by 9 years old. Other curricula don’t start for another 3-4 years. I always try to keep an asset based approach rather than a deficit based mindset when considering what my students know.
In saying this, I don’t want to be guilty of being too idealistic at the cost of students. Rightly or wrongly, our curricula are structured in such a way that, without procedural fluency by a certain time, it will really start having an impact. There is evidence to suggest that students without procedural fluency will continue to fall behind in their learning.
Secondly, and as you would know, students are hyper-aware of when they are being ‘babied’. There’s little point in giving a 14yo a multiplication worksheet that they saw 5-6 years ago. So we need to be strategic. As Jennifer Bay-Williams says, we need students to be put in the decision making position. And they need to practise this many times in many different contexts.
I can recommend ‘Multiplication by Heart’ for example. This is a flash cards game that pairs conceptual understanding with building automaticity. It also progresses with a student in order to meet them where they’re at. There’s a digital version also. Embedding the facts into game-based learning as part of a strategy, that can be really helpful in building procedural fluency. Getting students to drive their own learning in this way can be super effective.
In the spirit of trying to be practical and not just theoretical, here is a decent outline of how I might structure my students’ learning journey towards our example, procedural fluency of multiplication facts.
Let’s keep this conversation going as we work towards procedural fluency for all our students. Here’s a few resources at your fingertips now. Reach out for a full resource list.
Exploring mathematical fluency: teachers’ conceptions and descriptions of students by Katherin Cartwright
Figuring Out Fluency series by Jennifer M. Bay-Williams, John J. SanGiovanni
Make Math Moments: Ep197: Figuring Out Fluency – An Interview with Jennifer Bay-Williams
Math Fact Fluency Playground by Nicki Newton
Math is Figureoutable resources and podcast
Mathematical Education by William P. Thurston
Mathematical Fluency by Mike Askew
Multiplication by Heart Online Game.
NCTM position statements
Teaching Mathematics: Using research-informed strategies by Peter Sullivan
Join Our Community
Number Hive
How We Help
Resources
© Number Hive. All rights reserved.
Website made by Getmilk.